Theme: Smallest eigenvalues of large Hankel matrices at Critical point: Comparing a conjecture with parallelized computation

Speaker: Yang Chen, Professor                          

Host: Chengfa Wu, Research Scientist                          

Time: 11:00-12:00, January 11st, 2019                          

Venue: Conference Room 207, Office Building of SZU  

Talk Abstract:

The theorem of Berg, Chen and Ismail states that Classicalmoment problems are indeterminate if and only if the least eigenvalue of theHankel matrix generated by the moment problem is bounded away from 0 for all N, including Infinity.  

In this talk I will compare a conjecture (Chen-Lawrence) on the smallesteigenvalue of the Hankel form generated by the weight

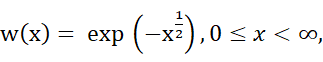
withthe numerical computation on the smallest eigenvalues, obtained from the HPCCof the University of Macau.

HPCC= High Performence Computing Cluster.

Hankel matrix

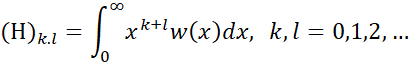
About the Speaker:

Yang Chen is currently a Professor of Mathematics in Department of Mathematics, University of Macau (UM). Prof. Chen got his BSc degree from National University of Singapore in 1981, followed by his master degree from Illinois Institute of Technology in 1983, a PhD degree from University of Massachusetts in 1987. After that, he did postdoctoral research work at Cavendish Laboratory and Karlsruhe University. From 1992 to 2012, Prof. Chen worked at Imperial College London and served as professor from 2003. He was awarded as the Chang Jiang Scholar of Ministry of Education in 2005. In 2012, Prof. Chen was appointed as a Professor of Mathematics in Department of Mathematics, University of Macau (UM). He has served as founding editor and editorial board member for Random Matrices: Theory and Applications and Member of Advisory Board for Journal of Physics A: Mathematical and General. The research interests of Prof. Chen lie on General Relativity, Statistical Mechanics of Polymers, Associated Electronic Systems, Random Matrix Theory and Orthogonal Polynomials. Prof. Chen currently studies on Random matrix theory and the relevant orthogonal polynomials. Prof. Chen has published 114 papers in international journals, such as J.Func. Anal.,Trans. Amer. Math. Soc.and Phys. Rev. Lett.